Question

Select the function that represents a parabola with vertex at (2,-1) and a point (5,8) on its curve

a.) f(x)=2(x+2)^2-1

b.) f(x)=(x+2)^2-1

c.) f(x)=(x-2)^2-1

d.) f(x)=2(x-2)^2-1

Answer 1

Correct answer is c.)
`f(x)=(x-2)^2-1`

Explanation:

The vertex form of a parabola can be written as following:

`y = a(x-h)^2 + k ....... (1)`

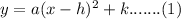
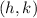`(h,k)` is the co-ordinate of vertex.

`a` is a constant whose positive or negative value decides where the parabola opens (up or down).

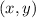`(x,y)` are the points on parabola.

`y` and
`f(x)` are interchangeable terms. We can use any of them.

For convenience with the co-ordinates in
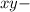`xy-`plane,
`y` is used here.

We are given that vertex is at (2,-1) and there is a point (5,8) on the curve.

i.e. h = 2 and k = -1,

x = 5 and y = 8

Putting the four values in equation (1):

`8 = a(5-2)^2 + (-1)\\\Rightarrow 8 = a(9) -1\\\Rightarrow 9 = 9a \\\Rightarrow a = 1`

Putting values of
`a` and
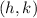`(h,k)` in equation (1) to find the equation of parabola:

`y=(x-2)^2-1`

As told earlier as well,
`y` and
`f(x)` are interchangeable terms.

So, correct equation of parabola is option C)
`f(x)=(x-2)^2-1`