Question

A ball of mass 1.00 kg is thrown at a door with velocity v1x = 12.0 m/s. The rectangular door has a mass of 30.0 kg and is 1.00 m wide. The ball strikes the door perpendicular to it, a horizontal distance 75.0 cm away from the hinges, and causes the door to swing open with an angular speed of 1.20 rad/s. What is the velocity v2x of the ball after striking the door? (The moment of inertia of a thin rectangular plate with mass M and dimensions a × b and the axis along the edge of length b is I = 1/3Ma2.)"

Answer 1

The velocity of the ball after collision is
`v_(2x) = -4 m/s`

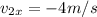
Step-by-step explanation:

From the question we are told that

The mass of the ball is
`m_b = 1.00\ kg`

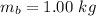
The velocity of the ball is
`v_(1x)= 12.0 \ m/s`

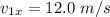
The mass of the rectangular door is
`m_d = 30 \ kg`

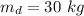
The width of the door is
`a = 1.00 \ m`

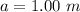
The distance of impact from the hinge is
`L = 75 \ cm = (75)/(100) = 0.75 \ m`

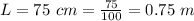
The angular speed of the door is
`w = 1.20 \ rad/s`

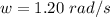
So the moment of inertia of the door is given from the question as

`I = (1)/(3) M a^2`

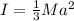
substituting values

`I = (1)/(3) * 30 * (1)`

`I = 10 \ kg \cdot m^2`

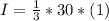
According to the law of angular momentum conservation

`L_i = L_f`

Where
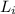`L_i` is the initial angular momentum of the system(the door and the ball) which is mathematically represented as

`L_i = m_b * v_(1x) + Iw_i`

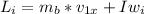
so
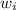`w_i` is the initial angular speed of the door which is zero

So

`L_i = m_b * v_(1x)`

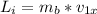
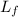`L_f` is the final angular momentum of the system(the door and the ball) which is mathematically represented as

`L_f = I w + m_b v_(2x) * L`

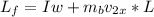
So

`m_b * v_(1x) = I w + m_b v_(2x) * L`

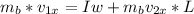
Substituting values

`1 * 12 * 0.75 = 10* 1.2 * v_(2x) * 0.75`

`v_(2x) = -4 m/s`

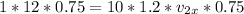
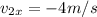
The negative sign show a reversal in the balls direction