Question

The 5th term in a geometric sequence is 160. The 7th term is 40. what are the possible values of the 6th term of the sequence?

A. +- 70
B. 70
C. +-80
D. 80

Answer 1

C.+- 80

Explanation:

Answer 2

We have been given that the 5th term in a geometric sequence is 160. The 7th term is 40. We are asked to find the possible values of 6th term of the sequence.

We know that an geometric sequence is in form
`a_n=a\cdot r^(n-1)`, where,

`a_n` = nth term of sequence,

a = First term,

r = Common ratio,

n = Number of terms.

We will get two equations using our given information as:

`160=a\cdot r ^(5-1)...(1)`

`160=a\cdot r ^(4)...(1)`

`40=a\cdot r ^(7-1)...(2)`

`40=a\cdot r ^(6)...(2)`

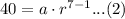
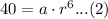
Upon dividing equation (2) by equation (1), we will get:

`(40)/(160)=(a\cdot r^6)/(a\cdot r^4)`

`(1)/(4)=r^(6-4)`

`(1)/(4)=r^(2)`

`r^(2)=(1)/(4)`

`\sqrt{r^(2)}=\pm\sqrt{(1)/(4)}`

`r=\pm(1)/(2)`

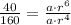
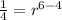
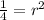
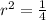
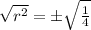
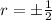
Let us solve for a.

`160=a\cdot ((-1)/(2))^(4)`

`160=a\cdot (1)/(16)`

`160\cdot 16=a\cdot (1)/(16)\cdot 16`

`2560=a`

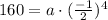
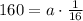
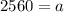
So our formula would be
`a_n=2560\cdot (\pm(1)/(2))^(n-1)`.

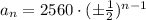We cannot determine whether the common ratio would be positive or negative, so we will take both values.

`a_6=2560\cdot (\pm(1)/(2))^(6-1)`

`a_6=2560\cdot (\pm (1)/(2))^(5)`

`a_6=2560\cdot \pm (1)/(32)`

`a_6=\pm 80`

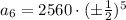
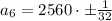
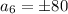
Therefore, the 6th term of the sequence would be
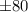`\pm 80` and option C is the correct choice.