Answers:
a) The equation is
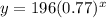
b) See image attachment below
c) See image attachment below
d) Week 10
=======================================================
Step-by-step explanation:
a)
One common template for an exponential equation is
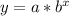 where 'a' is the starting amount and b is the growth or decay factor.
where 'a' is the starting amount and b is the growth or decay factor.
a = 196 is the starting amount of people who saw the movie per showtime
b = 1-0.23 = 0.77 is the decay factor. If the view count goes down by 23%, then we keep the remaining 77%
Therefore we go from
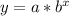 to
to
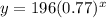
x = number of weeks
y = number of people, per viewing, who saw the movie for the particular week
--------------------
b)
Plug in x = 0 to find that y = 196
Plug in x = 1 to get y = 150.92 which rounds to y = 151 since we're talking about the number of people
Repeat for x = 2 all the way up to x = 9 to account for the first ten weeks. We stop at 9 instead of 10 because we started at x = 0.
The table is shown in the attachment below next to the graph.
I'm not sure why your teacher put a dollar sign over the second column of the table when it should be the number of people. It might be a typo. If they meant to do it, then there's missing information about ticket prices.
--------------------
c)
The graph is shown below. You can plot each (x,y) point on the same grid and then draw a curve through them. A much quicker way is to use software like GeoGebra (which is what I used) or Desmos or a pocket calculator. There are tons of many options to pick from. Feel free to choose your favorite.
The blue dashed segments on the graph visually help verify the result of part (d). We have y = 20 lead to an x value somewhere between x = 8 and x = 9. When submitting the graph to your teacher, you'll leave out the blue dashed segments.
--------------------
d)
Refer to the table we made in part (b). We have x = 9 lead to y = 19 approximately which is when y is below 20 people. Recall that x = 0 refers to week 1, so x = 9 refers to week 9+1 = 10. Week ten is where the view count drops below 20 people per showing.
If you wanted to use the graph in part (c), then you'd follow the blue dashed line mentioned earlier. Start at the y axis at y = 20. Trace the blue dashed line until reaching the curve. Then drop straight down to arrive somewhere between x = 8 and x = 9. Round up to x = 9. Then make the adjustment to go from x = 9 to week ten.
If you want an algebraic method, then follow the steps below.
Plug in y = 20 and solve for x. We'll need to involve logarithms to isolate the exponent.

This rounds up to x = 9 leading to week ten as the answer.
As confirmation
