Question

NO LINKS!!!

At the dance the DJ is blaring music at 110 decibels. As he fades the music, the sound level decreases about 16% every second.
How long until the sound level falls below 30 decibels? (SHOW WORK!)

Equation:_____________________

Answer: ______________________​

Answer 1

Equation:
`y=110(0.84)^x`

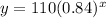
(where x is the time in seconds, and y is the sound level in decibels)

Answer: The sound level falls below 30 decibels after 7.452 seconds (3 dp)

Explanation:

We can model this as an exponential equation.

General form of an exponential equation:
`y=ab^x`

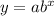
where:

• a is the initial value
• b is growth factor
• x is the independent variable
• y is the dependent variable

If b > 1 then it is an increasing function

If 0 < b < 1 then it is a decreasing function

If the sound decreases by 16% each second, then the growth (decay) factor will be 100% - 16% = 84% → 0.84

Given:

• a = 110 decibels
• b = decreases by 16% each second = 0.84
• x = time (in seconds)
• y = sound level (in decibels)

Substituting these values into the equation:

`\implies y=110(0.84)^x`

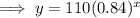
To find how long until the sound level falls below 30 decibels, set y < 30 and solve for x:

`\begin{aligned}110(0.84)^x & < 30\\\\(0.84)^x & < (3)/(11)\\\\\ln (0.84)^x & < \ln \left((3)/(11)\right)\\\\x \ln (0.84) & < \ln \left((3)/(11)\right)\\\\x & > (\ln \left((3)/(11)\right))/(\ln (0.84))\\\\x & > 7.452008851\end{aligned}`

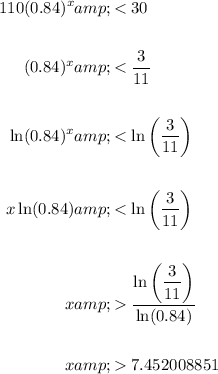
Therefore, the sound level falls below 30 decibels after 7.452 seconds (3 dp)

Answer 2

We are given:
Initial sound Intensity: 110 dB
Rate of decreasing sound level: 16% every second

Constructing the equation:
Since the Intensity decreases by 16% of it's current value every second.
Intensity(t) =
`110 * ((84)/(100))^(t)` [where t is the time elapsed]
In this equation, we multiply the initial sound intensity by 84% (since 16% was diminished).
because we are multiplying the same value by 84%, it will keep taking that percentage of the new value, which is what we need here because the music's intensity keeps becoming 84% of the previous value.

Time at which sound level falls to 30 dB:
replacing intensity by 30 in the equation we made.

`30 = 110 * ((84)/(100))^(t)`

`(3)/(11) = ((84)/(100))^t`
taking log of both sides.

`log((3)/(11)) = t*log((84)/(100))`

`\displaystyle (log((3)/(11)))/(log((84)/(100))) = t`

t = 7.452 seconds