Question

A park ranger at a large national park wants to estimate the mean diameter of all the aspen trees in the park. The park ranger believes that due to environmental changes, the aspen trees are not growing as large as they were in 1975.

Answer 1

(a) 0.15866

(b) Clustered, with two peaks

(c) Point estimate is 6.3 inches

Margin of error is 0.7 inches

(d) Yes

(e) Stratified sampling method

Explanation:

(a) The given information are as follows

Mean diameter of Aspen trees, μ = 8 inches

Standard deviation, σ = 2.5 inches

`z = (x - \mu)/(\sigma) = (5.5 - 8 )/(2.5) = -1`

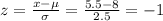
Therefore;

p(x < 5.5) = p(z < -1)

From the z score table, we have p = 0.15866

Therefore, the probability that a randomly selected aspen tree in this park in 1975 would have a diameter less than 5.5 inches = 0.15866

(b) The distribution of the Aspen trees can be described as clustered and having two peaks around 9.25 inches and 5.25 inches

(c) The point estimate is 5.6 + (7.0 - 5.6)/2 = 6.3

The margin of error = (7.0 - 5.6)/2 = 0.7 inches

(d) Yes, because the 8 inches is outside the range

(e) Stratified sampling method

Here, the Aspen trees are separated into the highland and lowland samples such that the measurement required will be representative of both highlands park and lowlands park.