Question

Suppose that the mean time that visitors stay at a museum is 94.2 minutes with a standard deviation of 15.5 minutes. The standard error of the mean,ox, is 3.1. A random sample of 25 of the times chosen. What interval captures 68% of the means for random samples of 25 scores?

Answer 1

`94.2 -0.994*3.1 = 91.1186`

`94.2 +0.994*3.1 = 97.2814`

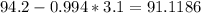
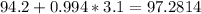
And the 68% confidence interval is given by (91.1186, 97.2814)

Explanation:

For this case we know that mean time that visitors stay at a museum is given by:

`\bar X = 94.2`

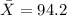
The standard deviation is given by:

`s= 15.5`

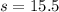
And the standard error is given by:

`SE = (s)/(√(n)) =3.1`

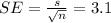
And we want to interval captures 68% of the means for random samples of 25 scores and for this case the critical value can be founded like this using the normal standard distribution or excel:

`z_(\alpha/2)= \pm 0.994`

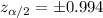
We can find the interval like this:

`\bar X \pm ME`

And replacing we got:

`94.2 -0.994*3.1 = 91.1186`

`94.2 +0.994*3.1 = 97.2814`

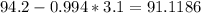
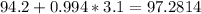
And the 68% confidence interval is given by (91.1186, 97.2814)