Question

A dietician believes that people who eat a high-fiber cereal as part of their breakfast will consume, on average, fewer calories at lunch than people who do not eat a high-fiber cereal as part of their breakfast. To test this claim, he measured the lunchtime calorie intake of 49 adults who did eat a high-fiber cereal for breakfast on a given day (group 1). For those individuals, the average number of calories consumed at lunch was 609.86, with a standard deviation of 55.96 calories. He also measured the lunchtime calorie intake of 78 adults who did not eat a high-fiber cereal for breakfast on a given day (group 2). For those individuals, the average number of calories consumed at lunch was 641.02, with a standard deviation of 109.14 calories. The dietician wishes to test this claim at the 5% significance level.

If Welch's two-sample test for equality of means is used, then what is the value of the test statistic tobs, rounded to two decimal places?

Answer 1

The calculated value Z = 1.8368 < 1.96 at 0.05 level of significance

The null hypothesis is accepted

The samples have been drawn from the same Population

Explanation:

Step(i):-

Given first sample size 'n₁' = 49

Mean of the first sample 'x₁⁻ = 609.86

Standard deviation of the sample S₁ = 55.96 calories

Given first sample size 'n₂' = 78

Mean of the first sample 'x₂⁻ = 641.02

Standard deviation of the sample S₂ = 109.14 calories

Step(ii):-

Null hypothesis : H₀: x₁⁻ = x₂⁻

Alternative Hypothesis : H₁: x₁⁻ ≠ x₂⁻

Level of significance ∝ = 0.05

Test statistic

`Z = \frac{x^(-) _(1)-x^(-) _(2) }{\sqrt{S.D^2((1)/(n_(1) ) }+(1)/(n_(2) ) }`

where

`S.D^(2) = (n_(1) S^2_(1)+ n_(2) S^2_(2) )/(n_(1) + n_(2) -2)`

`= (49 X (55.96)^2+ 78X(109.14)^2 )/(49 + 78 )`

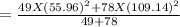
σ² = 8660.357

Step(iii):-

Test statistic

`Z = \frac{x^(-) _(1)-x^(-) _(2) }{\sqrt{S.D^2((1)/(n_(1) ) }+(1)/(n_(2) ) }`

`= \frac{ 609.86-641.02 }{\sqrt{8660.357((1)/(49 ) }+(1)/(78 ) ) }`

`Z = (-31.16)/(16.9638) = -1.8368`

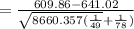
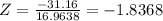
|Z| = |-1.8368| = 1.8368

The tabulated value Z₀.₉₅ = 1.96

The calculated value = 1.8368 < 1.96 at 0.05 level of significance

The null hypothesis is accepted

Final answer:-

The samples have been drawn from the same Population