Question

1) [25 pts] A 90-kg merry-go-round of radius 2.0 m is spinning at a constant speed of 20 revolutions per minute. A kid standing on the ground decides to bring the merry-go-round to rest and applies a force of 10.0 N tangentially to the merry-go-round. If the merry-go-round is modelled as a solid cylinder, (A) calculate its moment of inertia. (B) What is the angular acceleration of the merry-go-round? (C) How many revolutions will the merry-go-round complete until it finally stops?

Answer 1

(A) 180 kg·m²

(B) 0.111 rad/s²

(C) The number of revolutions the merry-go-round will complete until it finally stops is 3.142 or π rev

Step-by-step explanation:

The equation of the moment of inertia of a solid cylinder is presented as follows;

`I = (1)/(2)MR^2`

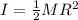
Where:

I = Moment of inertia of the merry-go-round

M = Mass of the merry-go-round

R = Radius of the merry-go-round

Therefore, I = 1/2×90×2² = 180 kg·m²

(B) For the angular acceleration we have;

Therefore, since the force × radius = The torque, we have, angular acceleration is found as follows

F × R = τ

10.0 × 2.0 = 20 = I×α = 180×α

α = 20/180 = 0.111 rad/s².

angular acceleration = 0.111 rad/s².

(C) Here we have ω₀ = 20 rev/ min = 20×2×π rad/min = π·40/60 rad/s

2/3·π rad/s

ω = ω₀ - α×t

∴ t = ω₀/α = (2/3·π rad/s)/(0.111 rad/s²) = 18.85 s

Hence we have

θ = ω₀·t + 1/2·α·t², plugging in the values, we have;

θ = 2/3·π×18.85 - 1/2·0.111·18.85²

θ = 19.74 rad

Therefore, since 2·π radian = 1 revolution

The number of revolutions the merry-go-round will complete until it stops is 19.74/(2·π) = 3.142 or π revolutions.