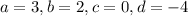Question

If you have a cubic polynomial of the form y = ax^3 + bx^2 + cx + d and lets say it passes through the points (2,28), (-1, -5), (4, 220), and (-2, -20) what would the coefficients a, b, c, and d equal? So confused, I'd greatly appreciate help! Thank you!

Answer 1

Explanation:

Step 1: Solve using the first point

(2, 28)

`28 = a(2)^3 + b(2)^2 + c(2) + d`

`28 = 8a + 4b + 2c + d`

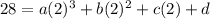
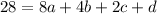
Step 2: Solve using the second point

(-1, -5)

`-5 = a(-1)^3 + b(-1)^2 + c(-1) + d`

`-5 = -a + b - c + d`

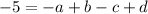
Step 3: Solve using the third point

(4, 220)

`220 = a(4)^3 + b(4)^2 + c(4) + d`

`220 = 64a + 16b + 4c + d`

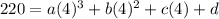
Step 4: Solve using the fourth point

(-2, -20)

`-20 = a(-2)^3 + b(-2)^2 + c(-2) + d`

`-20 = -8a + 4b - 2c + d`

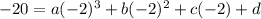
Step 5: Combine the first and fourth equations

`28 - 20 = 8a - 8a + 4b + 4b + 2c - 2c + d + d`

`8 = 8b + 2d`

`8 - 8b = 8b - 8b + 2d`

`(8 -8b)/2 = 2d/2`

`4 - 4b = d`

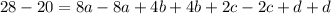
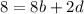
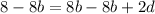
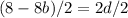
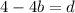
Step 6: Solve for c in the second equation

`-5 + 5 = -a + b - c + d + 5`

`0 + c = -a + b - c + c + d + 5`

`c = -a + b + d + 5`

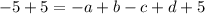
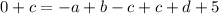
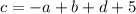
Step 7: Substitute d with the stuff we got in step 5

`c = -a + b + (4 - 4b) + 5`

`c = -a + b + 4 - 4b + 5`

`c = -a - 3b + 9`

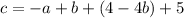
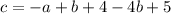
Step 8: Substitute d and c into the first equation

`28 = 8a + 4b + 2(-a - 3b + 9) + (4 - 4b)`

`28 = 8a + 4b - 2a - 6b + 18 + 4 - 4b`

`28 - 22 = 6a - 6b + 22 - 22`

`6 / 6 = (6a - 6b) / 6`

`1 + b = a - b + b`

`1 + b = a`

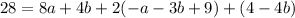
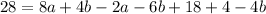
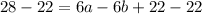
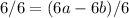
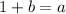
Step 9: Substitute a, b, and c into the third equation

`220 = 64(1 + b) + 16b + 4(-(1 + b) - 3b + 9) + (4 - 4b)`

`220 = 64 + 64b + 16b + 4(-1 - b - 3b + 9) + 4 - 4b`

`220 - 100 = 60b + 100 - 100`

`120 / 60 = 60b / 60`

`2 = b`

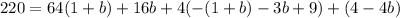
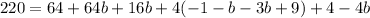
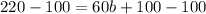
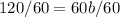
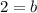
Step 10: Find a using b = 2

`a = b + 1`

`a = (2) + 1`

`a = 3`

Step 11: Find c using a = 3 and b = 2

`c = -a - 3b + 9`

`c = -(3) - 3(2) + 9`

`c = -3 - 6 + 9`

`c = 0`

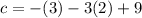
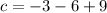
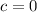
Step 12: Find d using b = 2

`d = 4 - 4b`

`d = 4 - 4(2)`

`d = 4 - 8`

`d = -4`

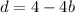
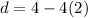
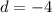
Answer:
`a = 3, b = 2, c = 0,d = -4`