Let's manipulate the expression a little bit and see what we come up with: we have
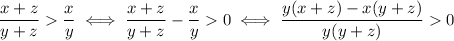
We can simplify the fraction as
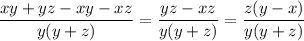
Since both
 and
and
 are positive, their sum will be positive as well. In other words, we can rewrite the fraction as
are positive, their sum will be positive as well. In other words, we can rewrite the fraction as
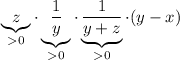
So, the sign of this fraction depends on the sign of
 . If its positive, then the whole fraction is positive (product of 4 positive factors). If it's negative, then the whole fraction is negative (product of 3 positive factors and a negative one).
. If its positive, then the whole fraction is positive (product of 4 positive factors). If it's negative, then the whole fraction is negative (product of 3 positive factors and a negative one).
In other words, we arrived to the desired conclusion:
