Answer:
Arc length is
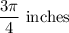
Explanation:
We have,
Central angle is 15 degrees and the radius of the circle measures 9 inches.
It is required to find the arc length of the sector.
The relation between arc length and the central angle is given by :
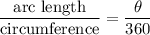
Circumference,
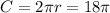
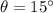
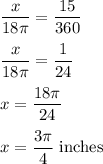
Hence, the correct option is (b).