Answer:
Yes, Elsa is correct.
Explanation:
The given equation is
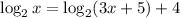
Elsa tries to solve the equation, and determines there is no solution. We need to check whether she is correct or not.
The given equation can be rewritten as

![[\because \log_aa^x=x]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/wqrs65y93d3ndbn25jmqu7r4je1j1mr3gf.png)
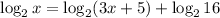
![\log_2x=\log_2[(3x+5)16]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/2ab0z6fft4xnn6tnu4c4wv53dsl2p7z2ku.png)
![[\because \log mn=\log m+\log n]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/bun7assppcisufrmd7m9ctkaulyspzez7u.png)
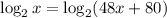
On comparing both sides, we get
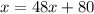
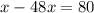
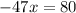
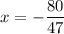
The value of x can not be negative because log is not defined for negative values.
Therefore, Elsa is correct and given equation have no solution.