Question

Which of the functions below have exactly

two distinct real zeros?
I. (v) = -12 + 14x – 45
II. 1.x) = 4x2 + 4
III. |(x) = 212 + 12x + 18
IV. /.x) = 3.x2 - 4x - 4
A. I and IV
C. II and III
B. I, II, and III
D. III and IV

Answer 1

A. I and IV

Explanation:

Solving a quadratic equation:

Given a second order polynomial expressed by the following equation:

`ax^(2) + bx + c, a\\eq0`.

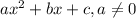This polynomial has roots
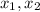`x_(1), x_(2)` such that
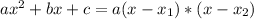`ax^(2) + bx + c = a(x - x_(1))*(x - x_(2))`, given by the following formulas:

`x_(1) = (-b + √(\bigtriangleup))/(2*a)`

`x_(2) = (-b - √(\bigtriangleup))/(2*a)`

`\bigtriangleup = b^(2) - 4ac`

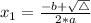
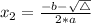
A quadratic equation has two distinct real zeros if:

`\bigtriangleup > 0`

So

I:
`f(x) = -x^(2) + 14x - 45`

`a = -1, b = 14, c = -45`

`\bigtriangleup = 14^(2) - 4*(-1)*(-45) = 16`

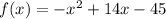
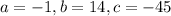
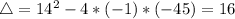
So function I has two distinct real zeros.

II:
`f(x) = 4x^(2) + 4`

`a = 4, b = 0, c = 4`

`\bigtriangleup = 0^(2) - 4*4*4 = -64`

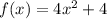
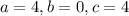
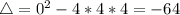
Negative, so II has no real zeros.

III:
`f(x) = 2x^(2) + 12x + 18`

`a = 2, b = 12, c = 18`

`\bigtriangleup = 12^(2) - 4*2*18 = 0`

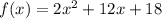
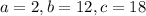
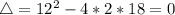
So III has one real zero with double multiplicity, that is, two equal zeros.

IV:
`f(x) = 3x^(2) -4x - 4`

`a = 3, b = -4, c = -4`

`\bigtriangleup = (-4)^(2) - 4*3*(-4) = 64`

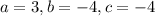
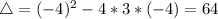
So function IV has two distinct real zeros.

So the correct answer is:

A. I and IV