Question

What is the center?
the circle passes through the point (-7,-7). what is the radius?​

Answer 1

We have been given image of circle that passes through point
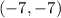`(-7,-7)`. We are asked to find the radius of the circle.

First of all, we will find the center of the circle.

We can see that center of circle is at point
`(-2,-1)`.

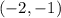Now we will use equation of circle to find radius.

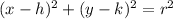`(x-h)^2+(y-k)^2=r^2`, where, point (h,k) represents center of circle and r represents radius of circle.

Now we will substitute the coordinates of point
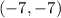`(-7,-7)` and coordinates of center
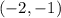`(-2,-1)` and solve for r as:

`(-7+2)^2+(-7+1)^2=r^2`

`(-5)^2+(-6)^2=r^2`

`25+36=r^2`

`61=r^2`

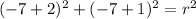
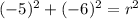
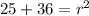
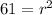
Switch sides:

`r^2=61`

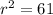
Now we will take positive square root on both sides:

`√(r^2)=√(61)`

`r=√(61)`

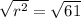
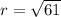
Therefore, radius of circle will be
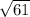`√(61)` and center is at point
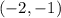`(-2,-1)`.