Question

Blast furnaces extra pure iron from the Iron(IIl)oxide in iron ore in a two step sequence. In the first step, carbon and oxygen react to form carbon monoxide:

2C(s)+O2(g) arrow 2CO(g)
In the second step, iron(lll) oxide and carbon monoxide react to form Iron and carbon dioxide:
Fe203(s) + 3CO(g) arrow 2Fe(s)+ 3CO2(g)
Suppose the yield of the first step is 71.% and the yield of the second step is 72.%. Calculate the mass of oxygen required to make 7.0 kg of iron.
Be sure your answer has a unit symbol, if needed, and is rounded to 2 significant digits.

Answer 1

5.9 kg

Step-by-step explanation:

We must work backwards from the second step to work out the mass of oxygen.

1. Second step

Mᵣ: 55.84

Fe₂O₃ + 3CO ⟶ 2Fe + 3CO₂

m/kg: 7.0

(a) Moles of Fe

`\text{Moles of FeO} = \text{7000 g Fe} * \frac{\text{1 mol Fe}}{\text{55.84 g Fe}} = \text{125 mol Fe}`

(b) Moles of CO

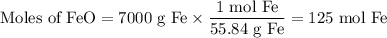
`\text{Moles of CO} = \text{125 mol Fe} * \frac{\text{3 mol CO}}{\text{2 mol Fe}} = \text{188 mol CO}`

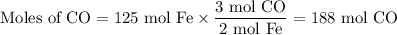
However, this is the theoretical yield.

The actual yield is 72. %.

We need more CO and Fe₂O₃ to get the theoretical yield of Fe.

(c) Percent yield

`\begin{array}{rcl}\text{Percent yield} &=& \frac{\text{ actual yield}}{\text{ theoretical yield}} * 100 \, \%\\\\ 72. \, \% & = & \frac{\text{188 mol}}{\text{actual yield}} * 100 \,\%\\\\0.72 &= &\frac{\text{188 mol}}{\text{actual yield}}\\\\\text{Actual yield} & = & \frac{\text{188 mol}}{0.72}\\& = & \textbf{261 mol}\\\\\end{array}`

We must use 261 mol of CO to get 7.0 kg of Fe.

2. First step

Mᵣ: 32.00

2C + O₂ ⟶ 2CO

n/mol: 261

(a) Moles of O₂

`\text{Moles of O}_(2) = \text{261 mol CO} * \frac{\text{1 mol O}_(2)}{\text{2 mol CO}} = \text{131 mol O}_(2)`

(b) Mass of O₂

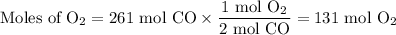
`\text{Mass of O}_(2)= \text{131 mol O }_(2) * \frac{\text{32.00 g O}_(2)}{\text{1 mol O}_(2)} = \text{4180 g O}_(2)`

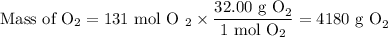
However, this is the theoretical yield.

The actual yield is 71. %.

We need more C and O₂ to get the theoretical yield of CO.

(c) Percent yield

`\begin{array}{rcl}71. \, \% & = & \frac{\text{188 mol}}{\text{actual yield}} * 100 \,\%\\\\0.71 &= &\frac{\text{4180 g}}{\text{actual yield}}\\\\\text{Actual yield} & = & \frac{\text{4180 g}}{0.71}\\\\& = & \text{5900 g}\\& = & \textbf{5.9 kg}\\\end{array}`

We need 5.9 kg of O₂ to produce 7.0 kg of Fe.