Question

The owners of Shaving Ice are concerned that many of their customers are starting to purchase their icy treats from Cold as Ice because of its new shaved-ice syrup, which has fewer grams of sugar than Shaving Ice. A random sample of 100 strawberry shaved ices from Shaving Ice found a mean of 22 grams of sugar and a standard deviation of 3.2 grams. A random sample of 100 strawberry shaved ices from Cold as Ice found a mean of 18 grams of sugar and a standard deviation of 2.1 grams. Which of the following formulas gives a 99% confidence interval for the difference in mean grams of sugar between a Shaving Ice strawberry shaved ice and a Cold as Ice strawberry shaved ice?

Answer 1

The correct option is;

`4\pm 2.63}\sqrt{(3.2^(2))/(100)+(2.1^(2))/(100)}`

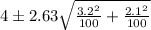
Explanation:

Here we have the formula for the confidence interval of the difference of two means where the population standard deviation is unknown based on the sample mean and sample standard deviation is given as follows;

`\left (\bar{x}_(1)- \bar{x}_(2) \right )\pm t_(\alpha /2)\sqrt{(s_(1)^(2))/(n_(1))+(s_(2)^(2))/(n_(2))}`

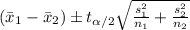
Where:

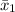`\bar{x}_(1)` = Mean of the first sample = 22 grams

`\bar{x}_(2)` = Mean of the second sample = 18 grams

s₁ = Sample standard deviation of the first sample = 3.2 grams

s₂ = Sample standard deviation of the second sample = 2.1 grams

n₁ = Sample size of the first sample = 100

n₂ = Sample size of the second sample = 100

`t_(\alpha /2)` = t value obtained from tables at 99% confidence level and 100 degrees of freedom = 2.626 = 2.63

Therefore, plugging in the values, we have;

`\left (22- 18 \right )\pm 2.63}\sqrt{(3.2^(2))/(100)+(2.1^(2))/(100)} = 4\pm 2.63}\sqrt{(3.2^(2))/(100)+(2.1^(2))/(100)}`

Therefore, the correct option is
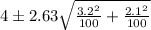`4\pm 2.63}\sqrt{(3.2^(2))/(100)+(2.1^(2))/(100)}`.