Question

How many strings can be formed by ordering the letters MISSISSIPPI which

contain no two I’s are consecutive ?

Answer 1

Total number of strings = 7350

Explanation:

Given:

MISSISSIPPI

Required:

Number of strings to contain no two consecutive I's

To do this, we start by calculating the number of strings that can be formed without any I;

We're left with MSSSSPP

7 characters in total

4 S and 2 P

The number of strings is calculated as follows

Number of strings =
`(7!)/(4!2!)`

Number of strings =
`(7*6*5*4!)/(4!*2*1)`

Number of strings =
`(7*6*5)/(2*1)`

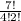
Number of strings = 7 * 3 * 5

Number of strings = 105

Then we count the number of possible spaces of I; This is as follows

-M-S-S-S-S-P-P-

This is represented by the - sign.

In total, there are 8 spaces, the 4 I's can occupy

There number of selection is as follows

`\left[\begin{array}{c}8&\\4&\\\end{array}\right] = (8!)/(4!*4!)`

`\left[\begin{array}{c}8&\\4&\\\end{array}\right] = (8 * 7 * 6 * 5 * 4!)/(4!*4*3*2*1)`

`\left[\begin{array}{c}8&\\4&\\\end{array}\right] = (8 * 7 * 6 * 5)/(4*3*2*1)`

`\left[\begin{array}{c}8&\\4&\\\end{array}\right] = 70`

Total number of strings = 105 * 70

Total number of strings = 7350