Answer:
C and D
Explanation:
We can go through and simplify each expression to figure out whether it has been simplified correctly.
A)
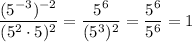
Not simplified correctly.
B)
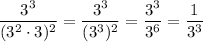
Not simplified correctly.
Since you know that both of these were not simplified correctly, you don't need to check the other two, since two of the answers are correct. Therefore, the answers are C and D. Hope this helps!