Question

A local retailer claims that the mean waiting time is less than 8 minutes. A random sample of 20 waiting times has a mean of 6.3 minutes with a standard deviation of 2.1 minutes. At α = 0.01, test the retailer's claim. Assume the distribution is normally distributed. Round the test statistic to the nearest thousandth.

Answer 1

The claim is not true

Explanation:

We are given that A local retailer claims that the mean waiting time is less than 8 minutes.

`H_0:\mu=8`

`H_a:\mu<8`

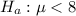
A random sample of 20 waiting times has a mean of 6.3 minutes with a standard deviation of 2.1 minutes.

`\bar{x}=6.3`

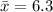
s = 2.1

n = 20

Since n <30 and population standard deviation is unknown

So,we will use t test

So,
`t=(x-\mu)/((s)/(√(n)))`

`t=(6.3-8)/((2.1)/(√(20)))`

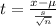
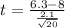
t=-3.62

α = 0.01

Degree of freedom = df=n-1=20-1=19

`t_{df,(\alpha)/(2)}=t_{19,(0.01)/(2)}=2.861`

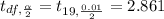
t calculated < t critical

So, we failed to reject null hypothesis

Hence the claim is not true