Question

Twenty-five adult citizens of the United States were asked to estimate the average income of all U.S. households. The mean estimate was x¯=$65,000 and s=$15,000 . (Note: The actual average household income at the time of the study was about $79,000 .) Assume the 25 adults in the study can be considered an SRS from the population of all adult citizens of the United States. A 95% confidence interval for the mean estimate of the average income of all U.S. households is

Answer 1

`65000-2.06 (15000)/(√(25))=58820`

`65000+2.06 (15000)/(√(25))=71180`

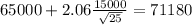
We are confident that the true mean for the average income of all U.S. households is between (58820;71180)

Explanation:

Information provided

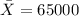`\bar X=65000` represent the sample mean for the average income of all US households

`\mu` population mean

s=15000 represent the sample standard deviation

n=25 represent the sample size

Confidene interval

The confidence interval for the true mean of interest is given by the following formula:

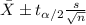`\bar X \pm t_(\alpha/2)(s)/(√(n))` (1)

The degrees of freedom are given by:

`df=n-1=25-1=24`

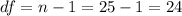
The Confidence level is is 0.95 or 95%, then the significance is
`\alpha=0.05` and
`\alpha/2 =0.025`, the critical value for this case would be
`t_(\alpha/2)=2.06`

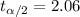
Replacing in formula (1) we got:

`65000-2.06 (15000)/(√(25))=58820`

`65000+2.06 (15000)/(√(25))=71180`

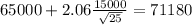
We are confident that the true mean for the average income of all U.S. households is between (58820;71180)