Question

A shoe manufacturer was investigating the weights of men's soccer cleats. He felt that the weight of these cleats was less than the average weight of 10 ounces. After a random sample of 13 pairs of cleats, he found that sample mean was 9.63 and the standard deviation was .585. At a significance level of .05, can it be concluded that the researcher was correct?

Show work

Answer 1

The conclusion is that the researcher was correct

Explanation:

From the question we are told that

The sample size is
`n = 13`

The sample mean is
`\= x = 9.63`

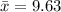
The standard deviation is
`s = 0.585`

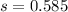
The significance level is
`\alpha = 0.05`

The Null Hypothesis is
`H_o : \mu = 0`

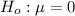
The Alternative Hypothesis is
`H_a = \mu < 10`

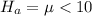
The test statistic is mathematically represented as

`t = (\= x - \mu )/((s)/(√(n) ) )`

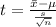
Substituting values

`t = (9.63 - 10 )/((0.585)/(√(13) ) )`

`t = - 2.280`

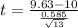
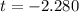
Now the critical value for
`\alpha` is

`t_(\alpha ) = 1.645`

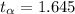
This obtained from the critical value table

So comparing the critical value of alpha and the test value we see that the test value is less than the critical value so the Null Hypothesis is rejected

The conclusion is that the researcher was correct