Question

A ball is thrown into the air with an upward velocity of 13 ft/s. Its height h in feet after t seconds is given by the function h = −2t^2+ 13t + 24. In how many seconds does the ball reach its maximum height?

Answer 1

3.25 seconds

Explanation:

The maximum height will occur when the velocity of the ball reaches zero in the air.

Velocity is given as the derivative of height, dh/dt.

The equation of height given is:

`h = -2t^2+ 13t + 24`

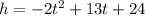
Differentiating height, h, with respect to time, t, we have:

`v = dh/dt = -4t + 13`

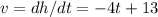
When v = 0:

`0 = -4t + 13\\\\=> 4t = 13\\\\t = 13 / 4 = 3.25 secs`

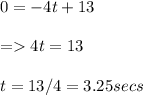
Therefore, it will take 3.25 seconds for the ball to reach maximum height.