Question

Question 1

Solve for
using the similar triangles. Round to the nearest tenth. (For example, 10.578 would round to 10.6)
Question 2
Find the height of the tree to the nearest whole meter using the two similar triangles below. (For example. 10.57
3 m
30 m​

Please answer fast thank you

Answer 1

1)x=21.33

2)Height of tree is 20 m

Explanation:

Question 1

ΔABC ≈ΔADE

Property of similar triangles :Corresponding sides of similar triangles are all in the same proportion

So,
`(AB)/(AD)=(BC)/(DE)\\(AB)/(AB+BD)=(BC)/(DE)\\(12)/(12+6)=(x)/(32)\\(12)/(18)=(x)/(32)\\(12)/(18) * 32 =x\\21.33=x`

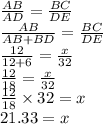
Question 2: Find the height of tree

ΔDEF ≈ΔDHI

Property of similar triangles :Corresponding sides of similar triangles are all in the same proportion

So,
`(DE)/(DH)=(EF)/(HI)\\(3)/(30)=(2)/(HI)\\HI=(2 * 30)/(3)\\HI=20`

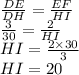
Hence The height of tree is 30 m