Answer:
Time taken is 0.897 sec and distance traveled is 56.36 mm
Explanation:
It is given radius of the coin r = 10 mm
Angle measure
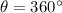
In radian it will be equal to
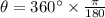
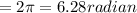
Angular velocity = 78 rev/sec
It is known that
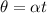
Therefore
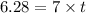
t = 0.897 sec
Now distance traveled will be equal to
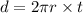
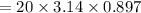
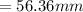
Therefore time taken is 0.897 sec and distance traveled is 56.36 mm