Answer:
The cost of a burger is $1.65 and the cost of a gatorade is $1.05.
Explanation:
We can solve this question using a system of equations.
I am going to say that:
x is the price of a burger.
y is the price of a gatorade.
6 burgers and 4 gatorades for $14.10
This means that

3 burgers and 4 gatorades for $9.15.
This means that

Will write 4y as a function of x.
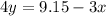
Replacing in the first equation:

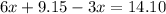
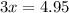
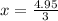
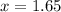
And
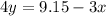

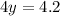

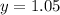
The cost of a burger is $1.65 and the cost of a gatorade is $1.05.