Answer:
a difference of squares
Explanation:
Let's write down the expression:

we can see that this expression is one of the form
 which is the general expression of a difference of squares.
which is the general expression of a difference of squares.
To be more specific and to see why we say this, let's make
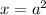 and
and

Now, if we substitute this in the general formula, we get:
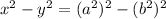
Thus, this expression is a difference of squares.