Answer:
Explanation:
I'll walk you through how to get the answers, but I'm not sure what your drop downs there are asking for. Maybe once you see the answers, you can figure out how to get the drop downs chosen correctly.
For your quadratic function, the h on the far left is how high the ball is after it is kicked and some amount of time has gone by, the -16t-squared part is the pull of gravity in feet per sec per sec, the 55t is the vertical velocity, and the 1 means that the ball was kicked when it was 1 foot off the ground. If we want to find when ("when" is a time measure) the ball was 45 feet off the ground, we sub in 45 for the h on the far left. Remember that that h is how high the ball is off the ground after it is kicked and some time has gone by. When we sub in 45 for that h, we will solve for t by factoring, to see at what times the ball is 45 feet from the ground.
It would be best to set up the equation and then plug it into the quadratic formula. Subbing in 45 for h gives us:
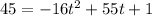 and we get everything on one side of the equals sign and set the quadratic equal to 0, giving us:
and we get everything on one side of the equals sign and set the quadratic equal to 0, giving us:
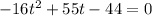 and then plug it into the quadratic formula with a = -16, b = 55, and c = -44:
and then plug it into the quadratic formula with a = -16, b = 55, and c = -44:
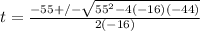 and we'll simplify that a little at a time:
and we'll simplify that a little at a time:
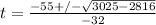 and
and
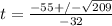 giving us 2 solutions:
giving us 2 solutions:
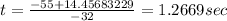 and
and
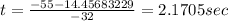
Let's interpret these solutions. When the ball is kicked up into the air, it experiences parabolic travel. It goes up to a certain max height until gravity wins and the ball comes back down to the ground. Everything thrown up into the air experiences parabolic (or projectile) motion (because gravity affects everything!). So the ball with reach a max height of some number of feet (you could find that out if you needed to, but we'll let that one go for now since this isn't physics class!) before it comes back down. On its way up to that max height, it will pass the 45 foot mark, and when it's coming back down, it will pass it again. The time that it passes the 45 foot mark going up is 1.2669 seconds after it is kicked. Then it goes up as high as it's going to and comes back down, passing the 45 foot mark on the way back down, at 2.1705 seconds after it was kicked.
However you need to use that interpretation to pick the correct drop-down answer is up to you. Much luck with your quadratics!! They're very important; you haven't seen the last of them by far!