Question

Maricopa's Success scholarship fund receives a gift of $ 115000. The money is invested in stocks, bonds, and CDs. CDs pay 5.75 % interest, bonds pay 5.8 % interest, and stocks pay 6.4 % interest. Maricopa Success invests $ 30000 more in bonds than in CDs. If the annual income from the investments is $ 6930 , how much was invested in each account?

Answer 1

Amount invested in CDs is $20000.

Amount invested in Bonds is $50000.

Amount invested in Stocks is $45000.

Explanation:

Let amount invested in CDs be $x.

Interest received from CDs is
`5.75 \%`

`\Rightarrow \text{Interest from CDs} = x * (5.75)/(100) ...... (1)`

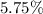
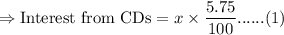
As per question, amount invested in bonds is $(x+30000).

Interest received from bonds is
`5.8 \%`.

`\Rightarrow \text{Interest from bonds} = (x+30000) * (5.8)/(100) ...... (2)`

Total amount is $115000.

So, amount invested in stocks = Total amount - Amount invested in CDs and Bonds

`\Rightarrow 115000 - x - (x+30000)\\ \Rightarrow (85000-2x)`

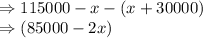
Interest received from stocks is
`6.4 \%`
`\Rightarrow \text{Interest from Stocks} = (85000-2x) * (6.4)/(100) ...... (3)`

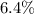
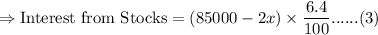
Total annual income from interest is $6930.

Adding equations (1), (2) and (3) and putting it equal to 6930.

`\Rightarrow x * (5.75)/(100) + (x+30000) * (5.8)/(100) + (85000-2x) * (6.4)/(100) = 6930\\\Rightarrow (12.8x - 11.55x) = 544000 + 174000 - 693000\\\Rightarrow 1.25x = 25000\\\Rightarrow x = 20000`

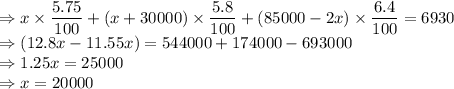
Amount invested in CDs is $20000.

Amount invested in Bonds is (x + 30000)= $20000+$30000 = $50000.

Amount invested in Stocks is
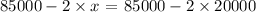`\(85000 - 2 * x\) = \(85000 - 2 * 20000\)`= $45000.