Answer:
Option A and C

Explanation:
Given equation
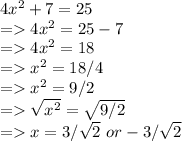
In the above problem after finding value for x^2 we have found the square root of 9 which is 3 and 2 which is

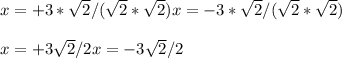
In the above equation we have rationalized the value of

as in answer
 is present in numerator and not in denominator.
is present in numerator and not in denominator.