Question

Oswego has a population of 7,800 people and is growing at a rate of 6% per year. Rye Brook

has a population of 9,400 people and is growing at a rate of 4% per year. In how many years, to

the nearest year, will Oswego have a greater population than Rye Brook? Show the

equation(s) or inequality you are solving.

Answer 1

We have been given that Oswego has a population of 7,800 people and is growing at a rate of 6% per year.Rye Brook has a population of 9,400 people and is growing at a rate of 4% per year.

We will use exponential growth function to represent population in both cities after x years.

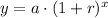`y=a\cdot (1+r)^x`, where

y = Final amount,

a = Initial amount,

r = Growth rate in decimal form,

t = Time.

`6\%=(6)/(100)=0.06`

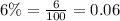
Population of Oswego after x years would be
`y=7,800(1+0.06)^x`.

`4\%=(4)/(100)=0.04`

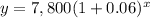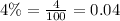
Population of Rye Brook after x years would be
`y=9,400(1+0.04)^x`.

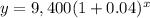Now we will set an inequality such as population of Oswego is greater than Rye Brook.

`7800\cdot(1.06)^t>9400\cdot (1.04)^t`

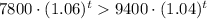
Let us take natural log on both sides.

`\text{ln}(7800\cdot(1.06)^t)>\text{ln}(9400\cdot (1.04)^t)`

`\text{ln}(7800)+\text{ln}((1.06)^t)>\text{ln}(9400)+\text{ln}((1.04)^t)`

`\text{ln}(7800)-\text{ln}(7800)+\text{ln}((1.06)^t)>\text{ln}(9400)-\text{ln}(7800)+\text{ln}((1.04)^t)`

`\text{ln}((1.06)^t)>\text{ln}((9400)/(7800))+\text{ln}((1.04)^t)`

`\text{ln}((1.06)^t)>\ln \left((47)/(39)\right)+\text{ln}((1.04)^t)`

`\text{ln}((1.06)^t)-\text{ln}((1.04)^t)>\ln \left((47)/(39)\right)+\text{ln}((1.04)^t)-\text{ln}((1.04)^t)`

`t\cdot \text{ln}(1.06)-t\cdot \text{ln}(1.04)>\ln \left((47)/(39)\right)`

`t(\text{ln}(1.06)-\text{ln}(1.04))>\ln \left((47)/(39)\right)`

`\frac{t(\text{ln}(1.06)-\text{ln}(1.04))}{\text{ln}(1.06)-\text{ln}(1.04))}>\frac{\ln \left((47)/(39)\right)}{\text{ln}(1.06)-\text{ln}(1.04))}`

`t>9.79546`

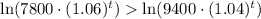
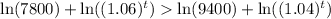
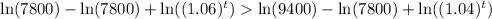
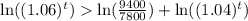
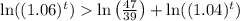
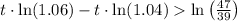
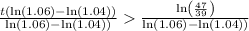
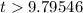
Therefore, in 10 years Oswego will have a greater population than Rye Brook.