Question

One of the primary goals of the Kepler space telescope is to search for Earth-like planets. Data gathered by the telescope indicates the existence of one such planet named Boralis orbiting a star 135 ly from our solar system. Consider an interstellar spaceship leaving Earth to travel to Boralis. The ship can reach 0.80c almost instantly and can also decelerate almost instantly. The ship is 143 m long in its reference frame.

1. What is the length of the moving ship (in m) as measured by observers on Earth?


2. How much time (in years) will it take for the spaceship to travel from Earth to Boralis, as measured by an observer on Earth?


3. How much time (in years) will it take for the spaceship to travel from Earth to Boralis, as measured by astronauts in the spaceship?

Answer 1

85.62 m

168.75 years

101.04 years

Step-by-step explanation:

`L_0` = Length of ship = 143 m

v = Velocity of ship = 0.8c

c = Speed of light

s = Distance to Boralis orbit = 135 ly

Gamma value

`\gamma=\frac{1}{\sqrt{1-(v^2)/(c^2)}}\\\Rightarrow \gamma=\frac{1}{\sqrt{1-(0.8^2c^2)/(c^2)}}\\\Rightarrow \gamma=1.67`

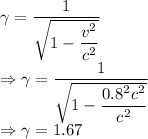
Length contraction is given by

`L=(L_0)/(\gamma)\\\Rightarrow L=(143)/(1.67)\\\Rightarrow L=85.62\ m`

The length is 85.62 m

Time taken

`t=(s)/(v)\\\Rightarrow t=(135)/(0.8)\\\Rightarrow t=168.75\ years`

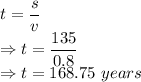
Time taken from the perspective one Earth is 168.75 years

Time dilation is given by

`t'=(t)/(\gamma)\\\Rightarrow t'=(168.75)/(1.67)\\\Rightarrow t'=101.04\ years`

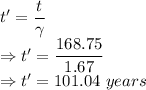
The time taken from the perspective of the ship is 101.04 years