Question

A 12-gallon container filled with water is being drained at a constant rate of 2 gallons per minute. The number off gallons of water,w, in the container t minutes after it begins to drain can be modeled by the equation w=12-2t.

Answer 1

The question is incomplete! Complete question along with answer and step by step explanation is provided below.

Question:

A 12-gallon container filled with water is being drained at a constant rate of 2 gallons per minute. Where t is the The number off gallons of water,w, in the container t minutes after it begins to drain can be modeled by the equation w=12-2t.

a) Write a formula that express w in terms of t.

b) As t increases from 2 to 5, w varies from __ to ___ ?

c) As t increases from 2 to 5, how much do t and w change by ?

Answer:

a)
`w = 12 - 2t`

b) As t increases from 2 to 5, w varies from 8 to 2 gallons.

c) As t increases from 2 to 5, t changes by 3 and w changes by -6.

Explanation:

a) We are given that a 12-gallon container filled with water is being drained at a constant rate of 2 gallons per minute.

Let w represents water and t represents time then we can write,

`w = 12 - 2t`

Since the water is being drained at rate of 2 gallons per minute that is why we have subtracted the term 2t from the initial capacity of the container that is 12 gallons.

b)

At t = 2

`w = 12 - 2(2)\\\\w = 12 - 4 \\\\w = 8 \: gallons`

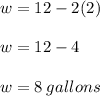
At = 5

`w = 12 - 2(5)\\\\w = 12 - 10 \\\\w = 2 \: gallons`

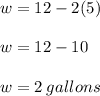
Therefore, as t increases from 2 to 5, w varies from 8 to 2 gallons.

c)

change in t

`\Delta t = 5 - 2\\\\\Delta t = 3`

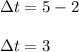
change in w

`\Delta w = 2 - 8\\\\\Delta w = -6`

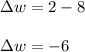
Therefore, as t increases from 2 to 5, t changes by 3 and w changes by -6.