Question

A bottling company fills bottles with a mean of 500 mL of liquia, with a

standard deviation of 2 mL. Quality control randomly samples 20

bottles at a time. Consider the mean volume of liquid in the sample

bottles. What is the standard deviation of the sampling distribution of

this sample mean?

Answer 1

The standard deviation of the sampling distribution of this sample mean is 0.447 ml.

Explanation:

We are given that a bottling company fills bottles with a mean of 500 ml of liquia, with a standard deviation of 2 ml. Quality control randomly samples 20 bottles at a time.

Let
`\bar X` = sample mean volume of liquid in bottles

The Sampling distribution of the sample mean also follows normal distribution;

As we know that ; Population mean =
`\mu` = 500 ml

Population Standard deviation =
`\sigma` = 2 ml

n = sample of bottles = 20

Now, the mean of sampling distribution is given by;

Sample Mean,
`\bar X` = Population mean = 500 ml

And, standard deviation of the sampling distribution of this sample mean is given by;

Standard deviation =
`(\sigma)/(√(n) )` =
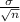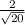`(2)/(√(20) )` = 0.447 ml

Hence, the standard deviation of the sampling distribution of this sample mean is 0.447 ml.