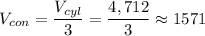Question

A cylinder and a cone have the same base and height. The cylinder can hold about 4,712 Centimeters cubed of sand. Jared says that the cone can hold about 1,178 Centimeters cubed of sand. Which explains whether Jared is correct?

A. Jared is correct because the volume of the cone is less than the volume of the cylinder. The cone holds 4,712 minus 1,178 = 3,534 centimeters cubed less sand than the cylinder.

B. Jared is correct because the cone and the cylinder have the same base and height so the cone holds StartFraction 4,712 Over 4 EndFraction = 1,178 centimeters cubedof sand.

C. Jared is not correct because the cone and the cylinder have the same base and height so the cone holds StartFraction 4,712 Over 3 EndFraction almost-equals 1,571 centimeters cubed of sand.

D. Jared is not correct because the volume of the cone cannot be found without knowing the radius of the base and the height of the cone.

Answer 1

C

Explanation:

Answer 2

C. Jared is not correct because the cone and the cylinder have the same base and height so the cone holds 4,712/3≈1,571 centimeters cubed of sand.

Explanation:

We have a cone and a cylinder with the same base and height.

We can express the volume of the cylinder as:

`V_(cyl)=\pi r^2H`

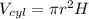
being r the radius and H the height.

The volume of the cone can be written as:

`V_(con)=(\pi)/(3)r^2H=(V_(cyl))/(3)`

As they have the same base and height, we know that the volume of the cylinder is 3 times the volume of the cone.

If the volume of the cylinder is 4,712 cm^3, then the volume of the cone is:

`V_(con)=(V_(cyl))/(3)=(4,712)/(3)\approx1571`