Question

A hotel chain wants to know if their customers are more satisfied with their service than the national average. The national average hotel satisfaction score is 87%. A survey of this hotel chains customers found that 108 out of 115 were satisfied with their service. Is this statistically significant evidence that this hotel chains customers are more satisfied with their service? Use an = .05

Answer 1

`z=\frac{0.939 -0.87}{\sqrt{(0.87(1-0.87))/(115)}}=2.20`

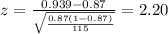
Now we can claculate the p value since is a right tailed test would be:

`p_v =P(z>2.20)=0.0139`

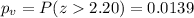
For this case since the p value is lower than the significance level provided
`\alpha=0.05` we have enough evidence to reject the null hypothesis and we can conclude that hotel chains customers are more satisfied with their service

Explanation:

Information given

n=115 represent the random sample selected

X=108 represent the number of people who were satisfied with their service

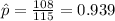`\hat p=(108)/(115)=0.939` estimated proportion of people who were satisfied with their service

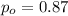`p_o=0.87` is the value that we want to test

`\alpha=0.05` represent the significance level

z would represent the statistic

`p_v` represent the p value

System of hypothesis

We want to verify if hotel chains customers are more satisfied with their service.:

Null hypothesis:
`p\leq 0.87`

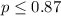
Alternative hypothesis:
`p> 0.87`

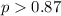
The statistic for this case is given by:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

Replacing the info given we got:

`z=\frac{0.939 -0.87}{\sqrt{(0.87(1-0.87))/(115)}}=2.20`

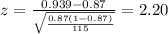
Now we can claculate the p value since is a right tailed test would be:

`p_v =P(z>2.20)=0.0139`

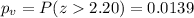
For this case since the p value is lower than the significance level provided
`\alpha=0.05` we have enough evidence to reject the null hypothesis and we can conclude that hotel chains customers are more satisfied with their service