Question

A large data sample of heights of US women is normally distributed with a mean height of 69.4 inches and a standard deviation of 2.6 inches.

What is the approximate probability that a randomly selected person in this sample is shorter than 66.8 inches?


A = 0.003

B= 0.025

C= 0.05

D= 0.16

E= 0.32

Answer 1

D) 0.16

The approximate probability that a randomly selected person in this sample is shorter than 66.8 inches

P(X< 66.8) = 0.16

Explanation:

Given data sample of heights of US women is normally distributed with a mean height of 69.4 inches and a standard deviation of 2.6 inches.

mean of the Population μ = 69.4 inches

Standard deviation of the Population σ = 2.6 inches

Let 'X' be the Random variable in Normal distribution

`Z = (x-mean)/(S.D)`

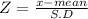
Here x = 66.8 , μ = 69.4 inches and σ = 2.6 inches

`Z = (66.8-69.4)/(2.6)`

Z = -1 < 0

The probability that a randomly selected person in this sample is shorter than 66.8 inches.

P(X< 66.8) = P( Z < -1)

= 1 - p(z > 1) ( by symmetry of normal curve)

= 1 - [ 0.5 + A(1)] [ A(-1) = A(1)]

= 0.5 - A(1)

= 0.5 -0.3413 (from normal table )

= 0.1587

P(X< 66.8) = 0.16

The approximate probability that a randomly selected person in this sample is shorter than 66.8 inches

P(X< 66.8) = 0.16