Question

A newly issued 10-year maturity, 6% coupon bond making annual coupon payments is sold to the public at a price of $730. The bond will not be sold at the end of the year. The bond is treated as an original-issue discount bond. a. Calculate the constant yield price. (Do not round intermediate calculations. Round your answer to 2 decimal places.) b. What will be an investor's taxable income from the bond over the coming year?

Answer 1

Yield price at year-end $746.55

taxable income: capital gain + coupon payment

16.55 + 60 = $76.55

Step-by-step explanation:

First we solve for the yield, which is the rate at which the discounted maturity and bond coupon payment matches the market price:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 60.000

time 10

rate 0.104863443

`60 * (1-(1+0.104863442947447)^(-10) )/(0.104863442947447) = PV\\`

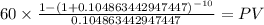
PV $361.0956

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity 1,000.00

time 10.00

rate 0.104863443

`(1000)/((1 + 0.104863442947447)^(10) ) = PV`

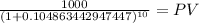
PV 368.90

PV c $361.0956

PV m $368.9045

Total $730.0001

So the market rate is 10.49%

Now we solve for the value of the bond at year-end:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 60.000

time 9

rate 0.104863443

`60 * (1-(1+0.104863442947447)^(-9) )/(0.104863442947447) = PV\\`

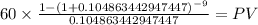
PV $338.9613

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity 1,000.00

time 9.00

rate 0.104863443

`(1000)/((1 + 0.104863442947447)^(9) ) = PV`

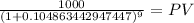
PV 407.59

PV c $ 338.96

PV m $ 407.59

Total $ 746.55