Answer:
Null hypothesis:
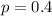
Alternative hypothesis:
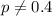
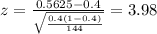

Since the p value is very low compared to the significance level we have enough evidence to reject the null hypothesis and we can conclude that the true percent of people with type A of blood is significantly different from 0.4 or 40%
Explanation:
Information given
n=144 represent the random sample taken
X=81 represent the number of people with type A blood
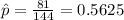 estimated proportion of people with type A blood
estimated proportion of people with type A blood
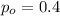 is the value that we want to verify
is the value that we want to verify
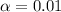 represent the significance level
represent the significance level
z would represent the statistic
![p_v{/tex} represent the p value </p><p><strong>Hypothesis to test</strong></p><p>We want to test if the percentage of the population having type A blood is different from 40%.: </p><p>Null hypothesis:[tex]p=0.4]()
Alternative hypothesis:
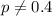
the statistic is given by:
 (1)
(1)
Replacing the info given we got:
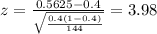
Now we can calculate the p value with this probability taking in count the alternative hypothesis:

Since the p value is very low compared to the significance level we have enough evidence to reject the null hypothesis and we can conclude that the true percent of people with type A of blood is significantly different from 0.4 or 40%