Question

The Colonel spots a campfire at a bearing N

22

∘

E from his current position. Sarge, who is positioned 353 feet due east of the Colonel reckons the bearing to the fire to be N

34

∘

W from his current position. Determine the distance from the campfire to each man, rounded to the nearest foot.

Answer 1

The distance from the Colonel to the campfire is 353 feet.

The distance from the Campfire to Sarge is approximately 395 feet.

Explanation:

Please see the attached image for the pictorial representation of the problem.

We are to determine the length AB and BC in the diagram.

The triangle formed is an Isosceles Triangle, therefore:

The distance from the colonel to the campfire is 353 feet.

Using Law of Sines

`(a)/(sinA) =(b)/(sinB) \\(a)/(sin68) =(353)/(sin56) \\aXsin56=353Xsin68\\a=(353Xsin68)/ sin 56\\a=394.79 feet`

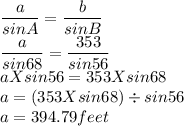
The distance from the Campfire to Sarge is approximately 395 feet.