Question

In a population where 77% of voters prefer Candidate A, an organization conducts a poll of 19 voters. Find the probability that 14 of the 19 voters will prefer Candidate A.

(Report answer accurate to 4 decimal places. That is, round to 4 decimal places.)

Answer 1

`P(X=14)=(19C14)(0.77)^(14) (1-0.77)^(19-14)=0.1928`

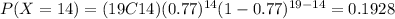
Then the probability that 14 of the 19 voters will prefer Candidate A is approximately 0.1928 or 19.28%

Explanation:

We can define X the random variable of interest "number of voters that will prefer Candidate A", since we have a sample size given and a probability of success we can use the binomial distribution to model the random variable. And on this case we can assume the following distribution:

`X \sim Binom(n=19, p=0.77)`

The probability mass function for the Binomial distribution is given by:

`P(X)=(nCx)(p)^x (1-p)^(n-x)`

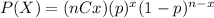
Where (nCx) means combinatory and it's given by this formula:

`nCx=(n!)/((n-x)! x!)`

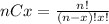
For this problem we want to find this probability:

`P(X=14)`

And usign the probability mass function defined before we got:

`P(X=14)=(19C14)(0.77)^(14) (1-0.77)^(19-14)=0.1928`

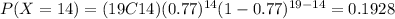
Then the probability that 14 of the 19 voters will prefer Candidate A is approximately 0.1928 or 19.28%