Answer:
The answer is in the explanation
Explanation:
Mean value =
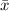 = 438
= 438
(a) The data appeared to be centered towards 438.
There are little or no skew.
There is no outliers.
(b) yes
(c) standard deviation = s = 14.8955
95% confidence interval =
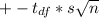
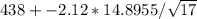 =
=
= (430.3415, 445.6585)
(d) Test statistic
t =
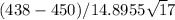
t = -3.3216
p -value is correctly given in option b.
No, 450 is not a plausible valaue.