Question

1) Consider the Cartesian equation of a hyperbola, y=±4√1+x^2/9, versus the parametric equations of the same hyperbola:

x = 3 tan t

y = 4 sec t.

What are the advantages of the parametric equations? Select all that apply. (3 points)

A. The parametric equations are easier to enter into a calculator for graphing.

B. The parametric equations show the direction in which the hyperbola is drawn.

C. The parametric equations describe a three-dimensional figure.

D. For a given value of the independent variable, the parametric equations yield exactly one point on the graph.

E. With parametric equations, each arm of the hyperbola is graphed in a continuous manner on a graphing calculator


2) Explain how you would graph the following set of parametric equations by plotting points and describing the orientation


3) For parametric equations x = a cos t and y = b sin t, describe how the values of a and b determine which conic section will be traced.

4) The following two sets of parametric functions both represent the same ellipse. Explain the difference between the graphs
x = 3 cos t and y = 8 sin t
x = 3 cos 4t and y = 8 sin 4t

Answer 1

Explanation:

1) Consider the cartesian equation of a hyperbola

`y= \pm4\sqrt{1+(x^2)/(9) }`

whose parametric equation are x = 3tan t and y = 4sec t

The parametric equation show the direction in which the parabola is drawn.

For a given value of the independent variable, the parametric equation yield exactly one point on the graph and

with parametric equations, each arm of the hyperbola is graphed in a continuous manner on the graphing calculator.

With parametric equation, the plotting becomes easier.

The cartesian equation of the hyperbola is a quadratic equation. So for a single x( or single y), there will be two values for y(or x). In parametric form, for a single 't', there will be only one point corresponding to that t.

2)

`If \left \{ {{x=3t} \atop {y= t^(2) }} \right. then t= (x)/(3) and y=( (t)/(3) )^2= (t^(2))/(9) .`

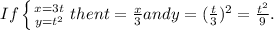
You can match points:

if x=0, y=0

if x=3, y=1

if x=-3, y=1

if x=6, y=4

if x=-6, y=4

The graph is in attached file

3)

Given that a conic section has parametric equations x= a cos t and y= b sin t,

Since only sum of squares of sin and cos =1 we find that out of conic sections, namely

parabola, circle, ellipse, hyperbola this can correspond only to ellipse or circle

Because parabola has only one variable in 2 degrees and hyperbola is difference of squares.

i) When a=b, we have this represents a circle with radius a.

ii) When a>b, we get an ellipse horizontal with major axis horizontal and centre at the origin and vertex at (a,0) (-a,0) (0,b) (0,-b)

iii) When a <b, we get a vertical ellipse with major axis as y axis and vertices same as

(a,0) (-a,0) (0,b) (0,-b)

4)

the main equation parametric of an ellipse is

x²/a² + y²/b² = 1

a≠0 and b≠0

let's consider x=3 cos t and y=8 sin t, these are equivalent to x²=9 cos²t and y²=64 sin²t, and imiplying x²/9=cos²t and y²/64=sin²t

therefore, x²/9+y²/64= cos²t+ sin²t, but we know that cos²t+ sin²t =1 (trigonometric fundamental rule)

so finally, x²/9+y²/64=1 equivalent of x²/3²+y²/8²= 1

this is an ellipse

with the same method, we found

x²/9+y²/64= cos²4t+ sin²4t =1, so the only difference between the graphs is the value of the angle (t and 4t)