Question

A manufacturer uses production method to produce steel rods. A random sample of 17 steel rods resulted in lengths with a standard deviation of 4.7 cm. at the 0.10 significance level, test the claim that the new production method has lengths with a standard deviation different from 3.5 cm, which was the standard deviation for the old method.

Use the traditional and confidence level methods to test this claim.

Answer 1

`\chi^2 =(17-1)/(12.15) 22.09 =15.87`

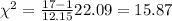
Traditional method

We can find a critical value in the chi square distribution with df =16 who accumulates
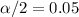`\alpha/2 =0.05` of the area on each tail and we got:

`\chi^2_(crit)= 7.962`

`\chi^2_(crit)=26.296`

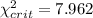
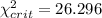
Since the calculated value is between the two critical values we don't have enough evidence to conclude that the true deviation is NOT significantly different from 3.5 cm

Confidence level method

We can find the p value like this

`p_v =2*P(\chi^2 >15.87)=0.92`

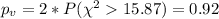
Since the p value is higher then the significance level we have enough evidence to FAIL to reject the null hypothesis and we can conclude that the true deviation is NOT significantly different from 3.5 cm

Explanation:

Data provided

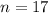`n=17` represent the sample selected

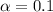`\alpha=0.1` represent the significance

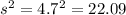`s^2 =4.7^2 =22.09` represent the sample variance

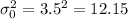`\sigma^2_0 =3.5^2 =12.15` represent the value to check

Null and alternative hypothesis

We want to verify if the new production method has lengths with a standard deviation different from 3.5 cm, so the system of hypothesis would be:

Null Hypothesis:
`\sigma^2 = 12.15`

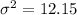
Alternative hypothesis:
`\sigma^2 \\eq 12.15`

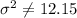
The statistic for this case is given by:

`\chi^2 =(n-1)/(\sigma^2_0) s^2`

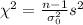
The degrees of freedom are:

`df =n-1= 17-1=16`

`\chi^2 =(17-1)/(12.15) 22.09 =15.87`

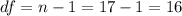
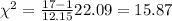
Traditional method

We can find a critical value in the chi square distribution with df =16 who accumulates
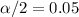`\alpha/2 =0.05` of the area on each tail and we got:

`\chi^2_(crit)= 7.962`

`\chi^2_(crit)=26.296`

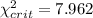
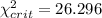
Since the calculated value is between the two critical values we don't have enough evidence to conclude that the true deviation is significantly different from 3.5 cm

Confidence level method

We can find the p value like this

`p_v =2*P(\chi^2 >15.87)=0.92`

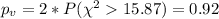
Since the p value is higher then the significance level we have enough evidence to FAIL to reject the null hypothesis and we can conclude that the true deviation is significantly different from 3.5 cm