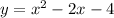Answer:
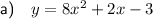
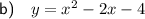
Explanation:
Given information:
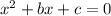
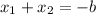
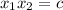
Part (a)

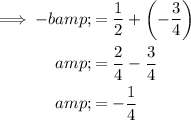
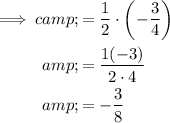
Substituting the found values of b and c into
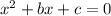
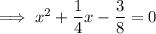
Multiply both sides by 8 so that coefficients are integers:
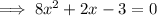
Therefore, the final quadratic equation is:
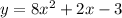
----------------------------------------------------------------------------------------------
Part (b)
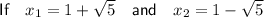
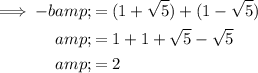
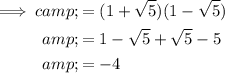
Substituting the found values of b and c into
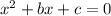
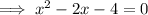
Therefore, the final quadratic equation is: