Question

A university wants to compare out-of-state applicants' mean SAT math scores (?1) to in-state applicants' mean SAT math scores (?2). The university looks at 35 in-state applicants and 35 out-of-state applicants. The mean SAT math score for in-state applicants was 540, with a standard deviation of 20. The mean SAT math score for out-of-state applicants was 555, with a standard deviation of 25. It is reasonable to assume the corresponding population standard deviations are equal.

At the 5% significance level, can the university conclude that the mean SAT math scores for in-state students and out-of-state students differ?
a. No, because the confidence interval contains zero
b. Yes, because the confidence interval contains zero
c. No, because the confidence interval does not contain zero
d. Yes, because the confidence interval does not contain zero

Answer 1

d. Yes, because the confidence interval does not contain zero.

Explanation:

We are given that the university looks at 35 in-state applicants and 35 out-of-state applicants. The mean SAT math score for in-state applicants was 540, with a standard deviation of 20.

The mean SAT math score for out-of-state applicants was 555, with a standard deviation of 25.

Firstly, the Pivotal quantity for 95% confidence interval for the difference between the population means is given by;

P.Q. =
`\frac{(\bar X_1-\bar X_2)-(\mu_1-\mu_2)}{s_p\sqrt{(1)/(n_1) +(1)/(n_2) } }` ~
`t__n__1-_n__2-2`

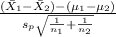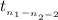
where,
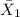`\bar X_1` = sample mean SAT math score for in-state applicants = 540

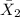`\bar X_2` = sample mean SAT math score for out-of-state applicants = 555

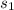`s_1` = sample standard deviation for in-state applicants = 20

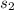`s_2` = sample standard deviation for out-of-state applicants = 25

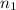`n_1` = sample of in-state applicants = 35

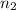`n_2` = sample of out-of-state applicants = 35

Also,
`s_p=\sqrt{((n_1-1)s_1^(2) +(n_2-1)s_2^(2) )/(n_1+n_2-2) }` =
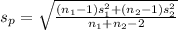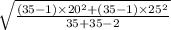`\sqrt{((35-1)* 20^(2) +(35-1)* 25^(2) )/(35+35-2) }` = 22.64

Here for constructing 95% confidence interval we have used Two-sample t test statistics.

So, 95% confidence interval for the difference between population means (
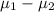`\mu_1-\mu_2`) is ;

P(-1.997 <
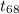`t_6_8` < 1.997) = 0.95 {As the critical value of t at 68 degree

of freedom are -1.997 & 1.997 with P = 2.5%}

P(-1.997 <
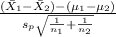`\frac{(\bar X_1-\bar X_2)-(\mu_1-\mu_2)}{s_p\sqrt{(1)/(n_1) +(1)/(n_2) } }` < 1.997) = 0.95

P(
`-1.997 * {s_p\sqrt{(1)/(n_1) +(1)/(n_2) } }` <
`{(\bar X_1-\bar X_2)-(\mu_1-\mu_2)}` <
`1.997 * {s_p\sqrt{(1)/(n_1) +(1)/(n_2) } }` ) = 0.95

P(
`(\bar X_1-\bar X_2)-1.997 * {s_p\sqrt{(1)/(n_1) +(1)/(n_2) } }` < (
`\mu_1-\mu_2`) <
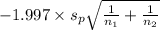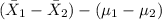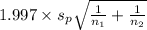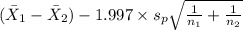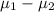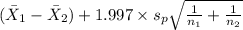`(\bar X_1-\bar X_2)+1.997 * {s_p\sqrt{(1)/(n_1) +(1)/(n_2) } }` ) = 0.95

95% confidence interval for (
`\mu_1-\mu_2`) =

[
`(\bar X_1-\bar X_2)-1.997 * {s_p\sqrt{(1)/(n_1) +(1)/(n_2) } }` ,
`(\bar X_1-\bar X_2)+1.997 * {s_p\sqrt{(1)/(n_1) +(1)/(n_2) } }` ]

=[
`(540-555)-1.997 * {22.64 * \sqrt{(1)/(35) +(1)/(35) } }`,
`(540-555)+1.997 * {22.64 * \sqrt{(1)/(35) +(1)/(35) } }`]

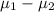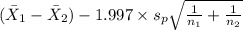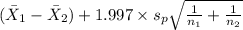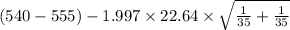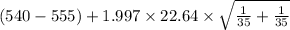= [-25.81 , -4.19]

Therefore, 95% confidence interval for the difference between population means SAT math score for in-state and out-of-state applicants is [-25.81 , -4.19].

This means that the mean SAT math scores for in-state students and out-of-state students differ because the confidence interval does not contain zero.

So, option d is correct as Yes, because the confidence interval does not contain zero.