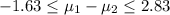Question

A simple random sample of 20 days in which Parsnip ate seeds was selected, and the mean amount of time it took him to eat the seeds was 14.5 seconds with a standard deviation of 3.98 seconds. An independent simple random sample of 17 days in which Parsnip ate pellets was selected, and the mean amount of time it took him to eat the pellets was 13.9 seconds with a standard deviation of 4.03 seconds. If appropriate, use this information to calculate and interpret a 90% confidence interval for the difference in the mean amount of time it takes Parsnip to eat seeds and the mean amount of time it takes Parsnip to eat pellets.

Answer 1

`(14.5-13.9) -1.69 \sqrt{(3.98^2)/(20)+ (4.03^2)/(17)} = -1.63`

`(14.5-13.9) +1.69 \sqrt{(3.98^2)/(20)+ (4.03^2)/(17)} = 2.83`

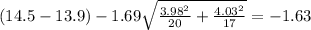
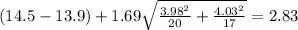
And the confidence interval for this case
`-1.63 \leq \mu_1 -\mu_2 \leq 2.83`

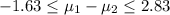
Explanation:

We know the following info from the problem

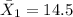`\bar X_1 = 14.5` sample mean for the group 1

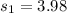`s_1 = 3.98` the standard deviation for the group 1

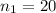`n_1= 20` the sample size for group 1

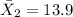`\bar X_2 = 13.9` sample mean for the group 2

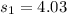`s_1 = 4.03` the standard deviation for the group 2

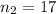`n_2= 17` the sample size for group 2

We have all the conditions satisifed since we have random samples.

We want to construct a confidence interval for the true difference of means and the correct formula for this case is:

`(\bar X_1 -\bar X_2) \pm t_(\alpha/2)\sqrt{(s^2_1)/(n_1) +(s^2_2)/(n_2)}`

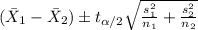
The degrees of freedom are given :

`df = n_1 +n_2- 2 = 20+17-2=35`

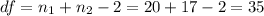
The confidence level is 0.9 or 90% and the significance level is
`\alpha=1-0.9=0.1` and
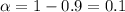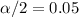`\alpha/2 = 0.05` and the critical value for this case is:

`t_(\alpha/2) = 1.69`

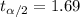
And replacing the info given we got:

`(14.5-13.9) -1.69 \sqrt{(3.98^2)/(20)+ (4.03^2)/(17)} = -1.63`

`(14.5-13.9) +1.69 \sqrt{(3.98^2)/(20)+ (4.03^2)/(17)} = 2.83`

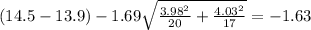
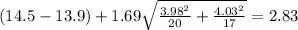
And the confidence interval for this case
`-1.63 \leq \mu_1 -\mu_2 \leq 2.83`