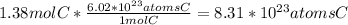Answer:
1.
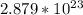 atoms of AgCl
atoms of AgCl
2.
 g of Bi
g of Bi
3.

Bonus:
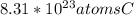
Step-by-step explanation:
1) If there are 68.54 grams of silver chloride, first know the chemical formula of silver chloride is AgCl. Then, you can use the molar mass of AgCl, found by adding the molar mass of its constituent elements on the periodic table, and unit conversions to solve for the amount of atoms of AgCl. Keep in mind that Avogadro's number states that there are
 atoms in one mole of a substance. Keep in mind that your answer will have four significant figures.
atoms in one mole of a substance. Keep in mind that your answer will have four significant figures.
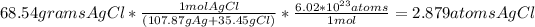
2) If there are
 atoms of bismuth, you can use the molar mass of Bi found on your periodic table and constants in order to calculate the mass of Bi.
atoms of bismuth, you can use the molar mass of Bi found on your periodic table and constants in order to calculate the mass of Bi.
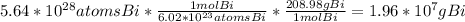
4) When asked for the empirical formula, recall that the empirical formula of a compound differs from its chemical formula, as the empirical formula is essentially the "greatest common factor" version of a chemical formula. For example, glucose,
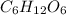 , and acetic acid,
, and acetic acid,
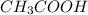 (or
(or
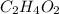 ) have different chemical formulas, but their empirical formulas are the same, represented as
) have different chemical formulas, but their empirical formulas are the same, represented as
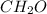 , where the greatest common factor 6 is factored out of glucose to obtain this formula, while the greatest common factor 2 is factored out of acetic acid.
, where the greatest common factor 6 is factored out of glucose to obtain this formula, while the greatest common factor 2 is factored out of acetic acid.
Given this information, you can imagine that there are 100g of carbon, hydrogen, and oxygen in this compound, so that the percentages given are easy to convert into mass. (Note that since empirical formula is a simplified form, the molar mass of the compound won't matter). This gives us a compound with 50.0g of carbon, 33.3g of oxygen, and 16.7g of hydrogen. We can then convert those values into moles:
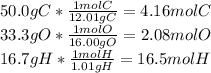
Now, you can express a formula for this compound as
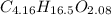 .
.
The lowest of these numbers is 2.08, or the number of moles of O in the formula. Dividing each of the subscripts by 2.08 will result in the following formula:
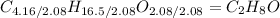
Note: Depending on if 1.00g/mol or 1.01g/mol was used for the molar mass of hydrogen, either 7.93 or 8.03 would be found to be the subscript of H. This is simply factored out by rounding either value to simply 8.
Bonus) Knowing that there are 25.6g of the substance in question, we can simply find 64.9% (the percent composition by mass of carbon for the unkown compound) of the total mass of the unknown compound.
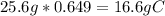
Now, simply use the molar mass of carbon, 12.01g/mol, to find the moles of carbon present.
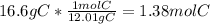
Now, using Avogadro's number, convert from moles to atoms. Keep in mind that your answer will have three significant figures.