Question

In a math class with 27 students, a test was given the same day that an assignment was due. There were 17 students who passed the test and 19 students who completed the assignment. There were 15 students who passed the test and also completed the assignment. What is the probability that a student who completed the homework failed the test?

Answer 1

The probability that a student who completed the homework failed the test is 0.211.

Explanation:

The probability of an event E is the ratio of the favorable number of outcomes to the total number of outcomes.

`P(E)=(n(E))/(N)`

The conditional probability of an event A given that another event B has already occurred is:

`P(A|B)=(P(A\cap B))/(P(B))`

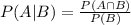
Denote the events as follows:

P = a student passes the test

F = a student fails the test

X = a student completes the assignment

Y = a student does not completes the assignment

From the information provided the summary table is as follows:

P F Total

X 15 4 19

Y 2 6 8

Total 17 10 27

Compute the probability that a student completed the assignment and failed the test as follows:

`P(X\cap F)=(n (X\cap F))/(N)=(4)/(27)`

Compute the probability that a student completed the assignment as follows:

`P(X)=\farc{19}{27}`

Compute the probability that a student failing the test given that the student completed the assignment as follows:

`P(F|X)=(P(X\cap F))/(P(X))=(4/27)/(19/27)=(4)/(19)=0.21053\approx 0.211`

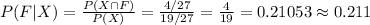
Thus, the probability that a student who completed the homework failed the test is 0.211.