Answer:
The mass of the sample after six days will be of 319.24 grams.
Explanation:
The exponential growth model for the mass of a substance after t days is:
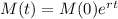
In which M(0) is the initial mass and r is the increase rate, as a decimal.
A sample increases continuously at a relative rate of 11% per day.
This means that
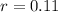
Find the mass of the sample after six days if there were 165 grams of the substance present at the beginning of the study.
This is M(6) when M(0) = 165.
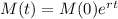
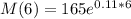
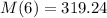
The mass of the sample after six days will be of 319.24 grams.